avatar
Published on

Pytorch (2-1) - 다층 퍼셉트론

Author
  • avatar
    Name
    yceffort

전에는 신경망에서 중간층을 하나로만 했지만, 이 중간층을 여러개로 늘린 것을 심층신경망 (deep neural network) 라고 한다. 벌써 부터 뭔가 있어보인다. 이는 딥러닝에서 주요 매커니즘이다. 신경망과 심층 신경망 모두 퍼셉트론을 여러개 조합해서 구성한 것으로, 다층 퍼셉트론 (multilayer perceptron, MLP)라고 한다.

어쩄거나, 입력층, 중간층, 출력층으로 구성되어 있는 것은 똑같다. 다만 차이점은 중간층이 여러개라는 것 뿐이다.

multi-layer-perceptron

마찬가지로, 순전파와 역전파를 반복해서 학습이 이뤄지며 모형을 생성한다. 다만 중간층이 여러개라는 차이점과 함께 또다른 차이가 있는데, 바로 학습 이전단계에 노드간 연결의 가중치를 조절하는 사전 학습을 거친다는 차이가 있다.

사전 학습 알고리즘으로는, 자기부호화기(Autoencoder)가 유명하다.

자기 부호화기

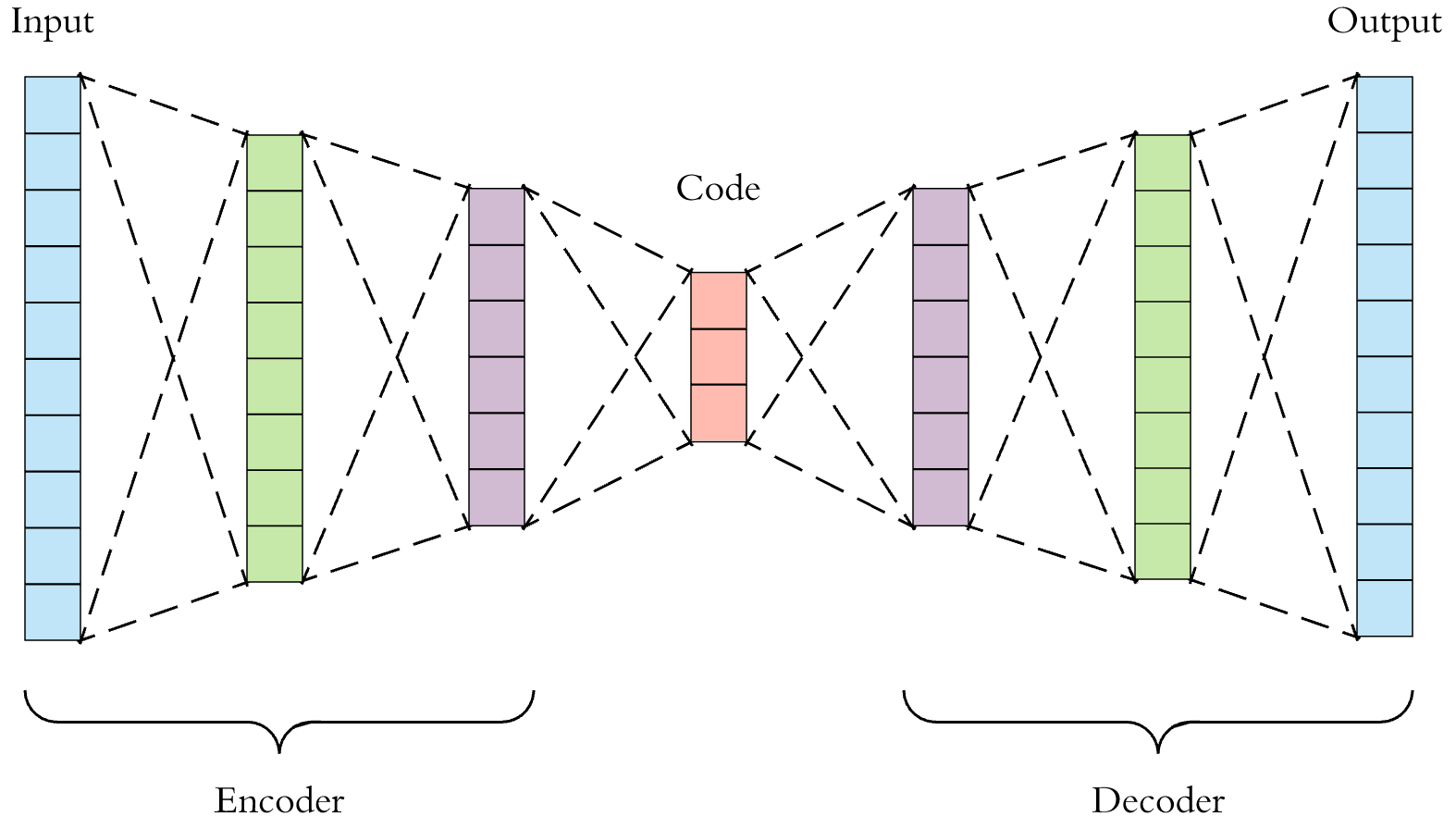
auto-encoder

자기부호화기는 다층 퍼셉트론 처럼 입력층, 중간층, 출력층으로 구성된다. 다만 입력층과 출력층의 노드 수가 같아야 하며, 비지도학습, 차원축소에 쓰이는 알고리즘이므로 설명변수만으로 구성되어 있다.

그리고 순전파와 역전파를 반복하면서 출력값과 입력값이 비슷해지도록 (자기 자신을 재현하도록) 학습하고 모형을 생성한다. 이 때 입력층과 중간층에서는 정보 압축 (encoding)이 일어나고, 중간층과 출력층 사이에서는 복호화 (decoding)이 일어난다.

자기 부호화기를 이용하면, 다층 퍼셉트론을 한층씩 쌓아 올릴 수 있다.

최적화 기법

이전에는 최적화 기법으로 경사하강법을 사용했다. 이 밖에도 momentum, adam 등이 있는데, 특히 adam을 많이 사용한다. 경사하강법에서는 학습률이 고정이었지만, adam에서는 학습도중에 자동으로 학습률을 자동으로 조정한다. (오오..) 따라서 좀더 효율적인 학습이 가능하다.

최적화의 효과를 더 높이기 위한 방법도 있다. 가중치 감쇠는 가중치에 계수를 곱해서, 가중치 값이 크게 발산하는 현상을 방지, 최적화가 안정적으로 진행되게 한다. 배치 정규화는 미니배치의 평균과 분산값으로 각층 노드의 값을 평균 0, 분산 1이 되도록 표준화 해서학습 속도를 개선한다.

과적합 (Overfitting)

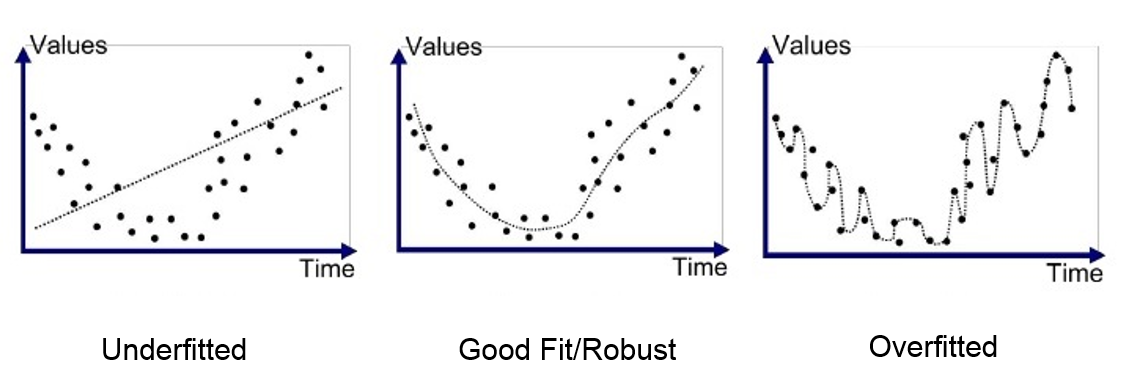
over-fitting

와인 분류하기 2

이번엔 다층 퍼셉트론으로 와인을 분석해보자. 텐서로 변환하고, 준비하는 과정까지는 똑같다.

import torch
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset

from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split

import pandas as pd

wine = load_wine()
wine_data = wine.data[0:130]
wine_target = wine.target[0:130]

train_X, test_X, train_Y, test_Y = train_test_split(wine_data, wine_target, test_size=0.2)

# 데이터를 텐서 형태로 변환
train_X = torch.from_numpy(train_X).float()
train_Y = torch.from_numpy(train_Y).long()

test_X = torch.from_numpy(test_X).float()
test_Y = torch.from_numpy(test_Y).float()

train = TensorDataset(train_X, train_Y)

신경망 구성

class Net(nn.Module):

  def __init__(self):
    super(Net, self).__init__()
    self.fc1 = nn.Linear(13, 96)
    self.fc2 = nn.Linear(96, 96)
    self.fc3 = nn.Linear(96, 96)
    self.fc4 = nn.Linear(96, 96)
    self.fc5 = nn.Linear(96, 96)
    self.fc6 = nn.Linear(96, 2)


  def forward(self, x):
    x = F.relu(self.fc1(x))
    x = F.relu(self.fc2(x))
    x = F.relu(self.fc3(x))
    x = F.relu(self.fc4(x))
    x = F.relu(self.fc5(x))

    x = self.fc6(x)

    return F.log_softmax(x)


model = Net()

계산은 똑같다.

#오차함수
criterion = nn.CrossEntropyLoss()

#최적화 담당
optimizer = optim.SGD(model.parameters(), lr=0.01)

#학습 300회 ㄱㄱ
for epoch in range(300):
  total_loss = 0

  for train_x, train_y in train_loader:
    train_x, train_y = Variable(train_x), Variable(train_y)

    #경사 초기화
    optimizer.zero_grad()

    #순전파
    output = model(train_x)

    #오차
    loss = criterion(output, train_y)

    #역전파 계산
    loss.backward()

    #가중치 업데이트

    optimizer.step()

    #총 오차 업데이트
    total_loss += loss.data.item()


  if (epoch + 1) % 50 == 0:
    print(epoch + 1, total_loss)

test_x, test_y = Variable(test_X), Variable(test_Y)
result = torch.max(model(test_x).data, 1)[1]
accuracy = sum(test_y.data.numpy() == result.numpy()) / len(test_y.data.numpy())
accuracy

결과: 0.8846153846153846

와 88%! 이번에는 좀 쓸 만해졌다.

Issue on GitHub